- Who is 1QBit?
- What is the Market Sentiment Meter (MSM)?
- How is the MSM Calculated?
- What does the MSM look like on a real product?
- Are there risks in using the MSM to measure risk?
- What type of data does 1QBit provide?
- What is the file format of the 1QBit data?
- What is the average daily file size?
- How many files are available per day?
- What is the delivery frequency of the data?
- What time is delivery time of the data each day?
- Are files compressed?
- Are sample files available?
- How far back historically is data available?
- Where does the futures settlement price and volume data come from?
- What settlement price is used on days that a market is closed?
- How does the roll from an expiring month affect the definition of the nearby month and other calculations, such as day-to-day return?
- Why is there sometimes no high or low price data in the second futures contract columns?
- What is a smoothed time series? How does long-term differ from short-term?
- What does the volume data include?
- How is historical volatility calculated?
- How are moving averages calculated?
- What are the descriptive parameters of the risk-return probability distribution?
- How are the probabilities of reaching price targets calculated?
- Data Structure
1QBit is a software company focused on solving intractable industry problems with the most advanced quantum and classical hardware available. 1QBit is backed by major corporations including Accenture, Allianz, CME Group, Fujitsu, Royal Bank of Scotland and the Siam Commercial Bank. Its hardware partners include D-Wave, Fujitsu, IBM, Microsoft, Rigetti and others. 1QBit’s publicly-announced client list includes DowDuPont, Biogen and NatWest.
1QBit’s 60+ researchers and developers hold over 100 university degrees in a wide variety of specialized areas including medicine and biology, machine learning, computational physics, chemistry, mathematics, computer science, business and engineering. 1QBit develops algorithms in a variety of fields and applies the synergies that occur when concepts and techniques cross from one field to another. This includes the analysis of market sentiment based on volume, price and open interest data available from sources like CME DataMine.
The Market Sentiment Meter is organized around the concept that typical bell-shaped risk-return probability distributions seriously underestimate tail risk and that just augmenting the tails of the distribution is not necessarily sufficient.
As an illustration, take event risk where traders might imagine two dissimilar outcomes. For example, since 2016, we have seen event risk associated with elections – UK Brexit Referendum of June 2016, U.S. Presidential election of November 2016, French and UK elections in 2017, Brazilian elections of October 2018, U.S. Congressional elections of November 2018, etc., where there were two possible scenarios. Before the event, the market typically prices the probability-weighted outcome, or the middle ground. After the event, when the outcome becomes known, the market immediately moves away from the middle ground to the “winning” scenario – a price break. For example, with Brexit, the leave vote generated a sharp downward move in the British pound (versus USD), while a Remain vote would have presumably generated a sharp almost instantaneous rally in the pound – either way, the pound was no longer going to trade in the middle.
To handle risk-return probability distributions that may not have bell-shaped curves and may be highly asymmetric, the MSM method uses a mixture distribution process, and gathers a variety of information from futures and options prices, volumes and intra-day activity to create a proxy for the actual unobservable distribution. While implied volatility from options prices is one of the metrics used in the MSM process, it is not the sole primary driver of the process and it is not allowed to bias the results toward bell-shaped solutions.
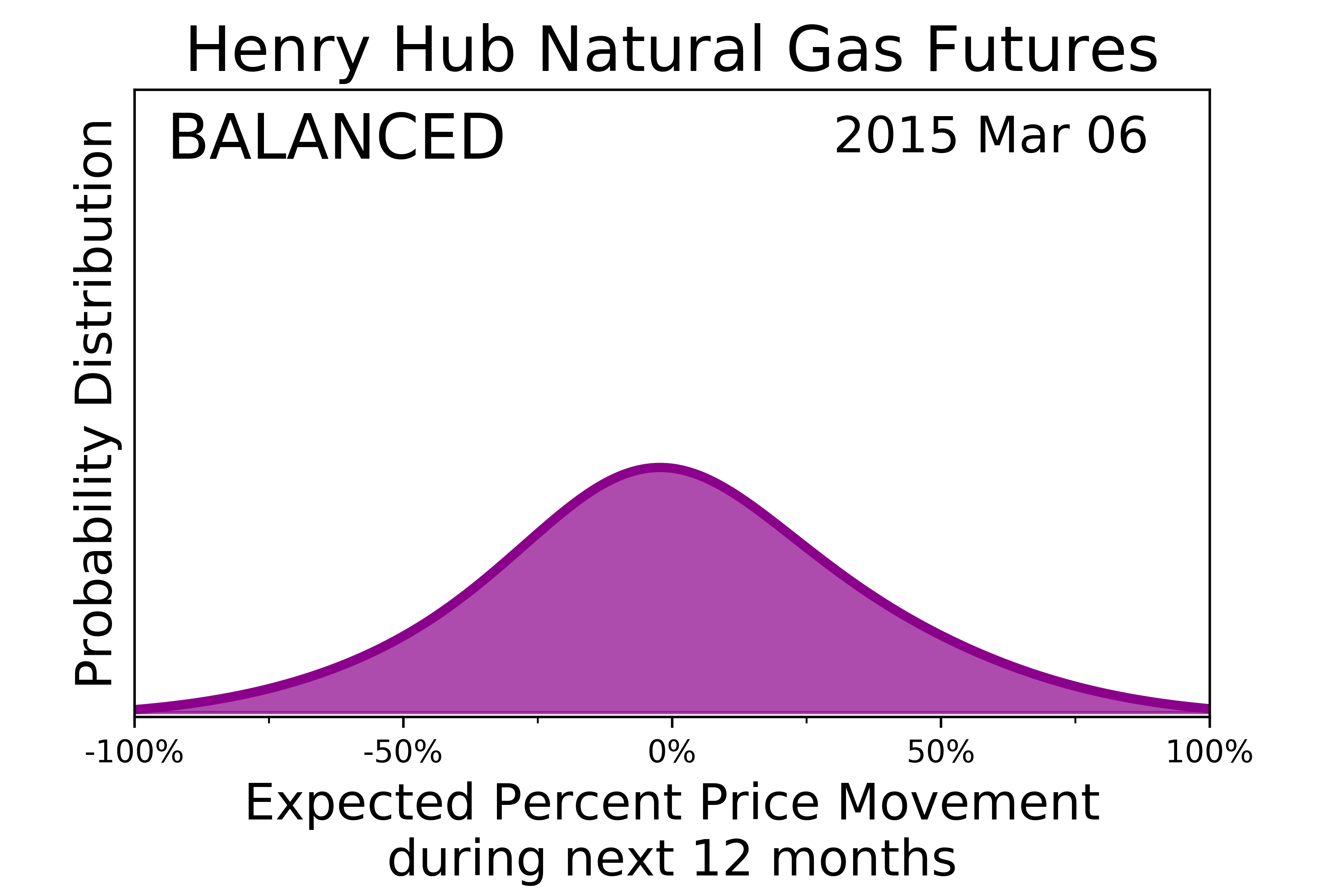
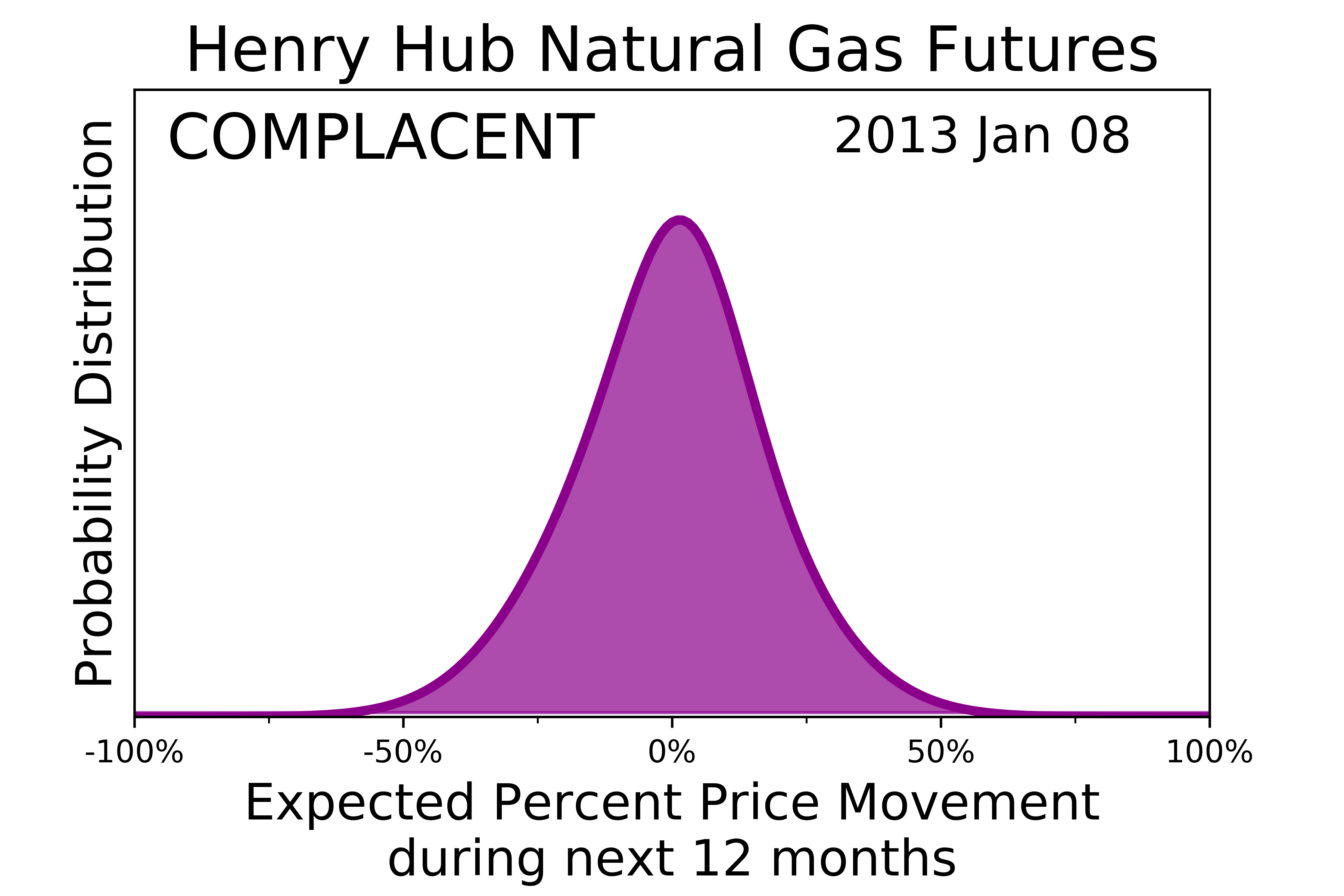
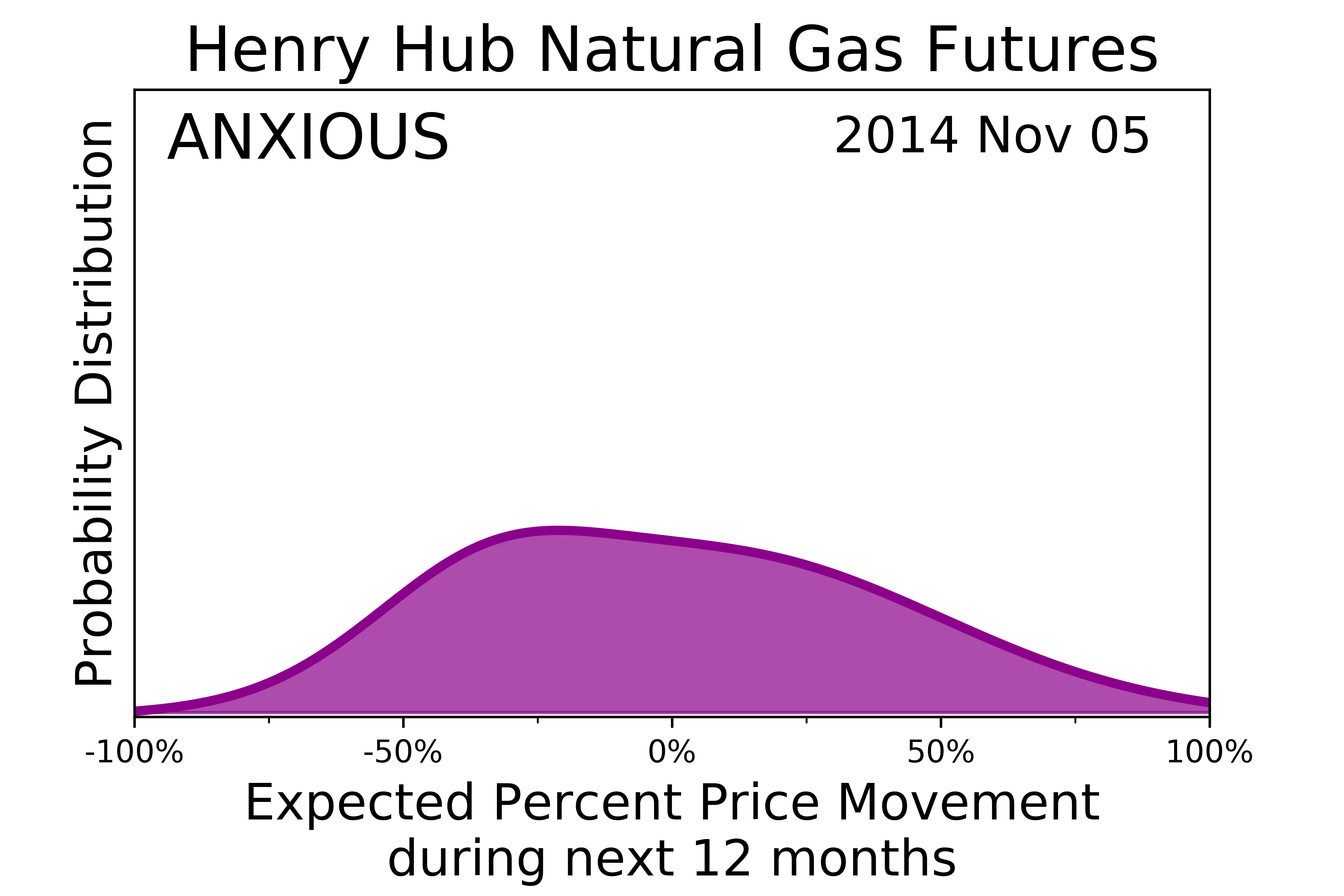
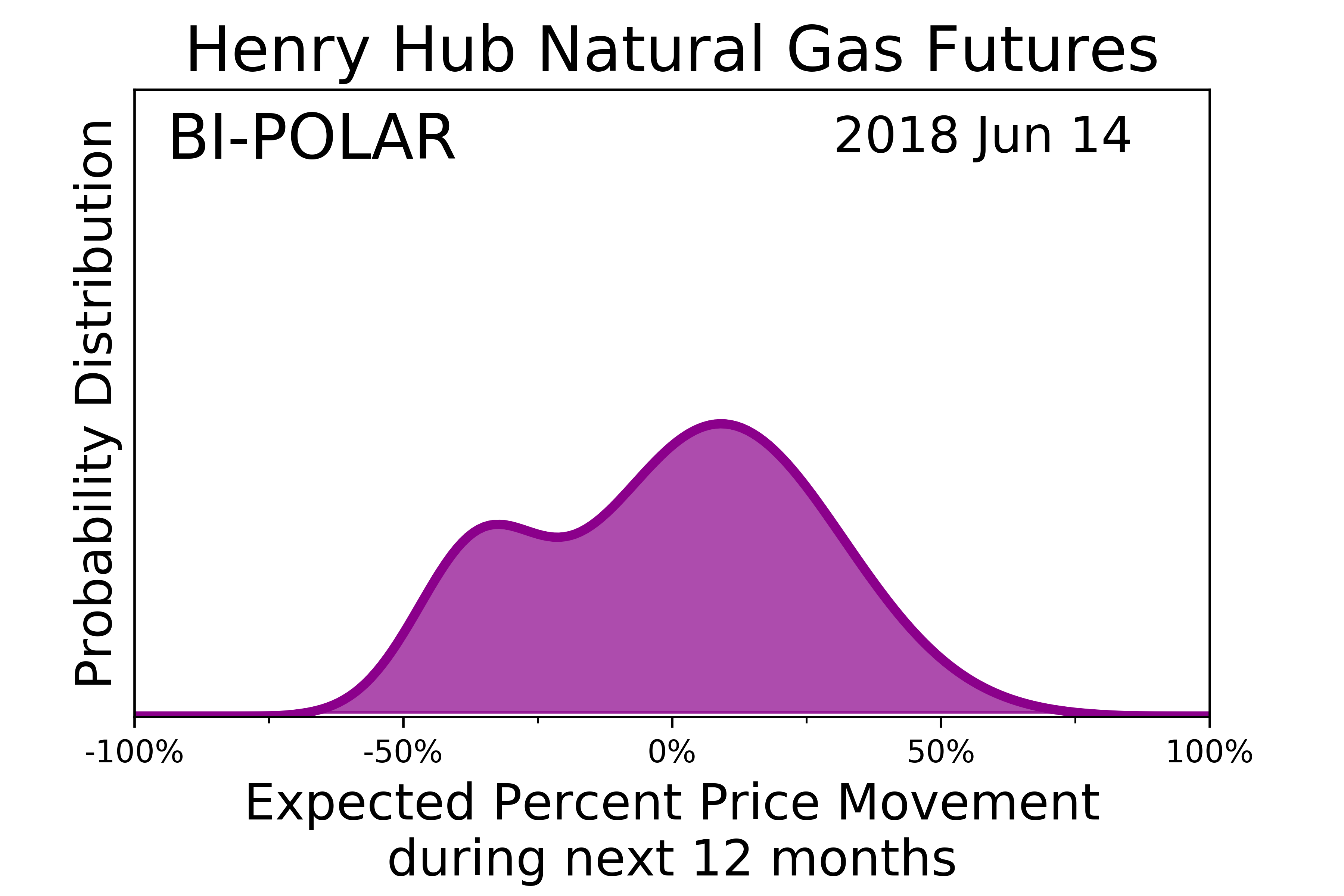
The MSM risk-return probability distribution has the four characteristic shapes shown below.
Balanced risk is the most common state and shows a bell-shaped risk-return probability distribution. |
|
Complacent is when the risk-return probability distribution is tall and narrow. Market participants have relatively few worries. |
|
Anxious is when the distribution broadens and may even move off-center. Market participants see worries everywhere. |
|
Bi-Polar or Event Risk occurs when market participants are weighing the probabilities of two starkly different outcomes and the distribution has two modes. Bi-polar states are rare and typically short-lived, yet extremely important to recognize. |
The MSM risk-return probability distribution is calculated using a proprietary process based on multiple metrics from the price, volume and intra-day activity of futures and options markets. Read our research paper on “Reimagining Probability Risk Distributions,” for an intuitive explanation of our process.
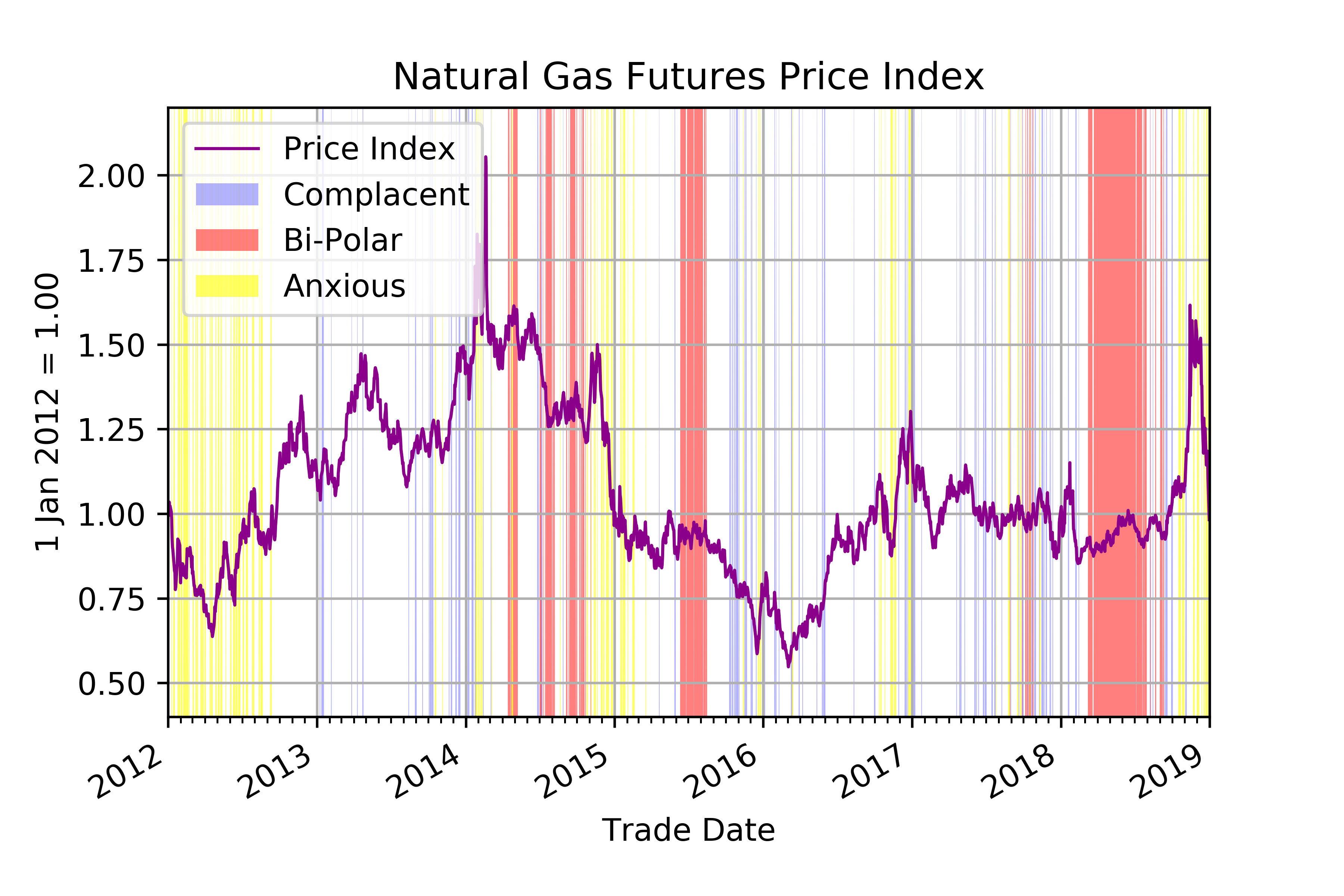
The time series below shows the states of the Market Sentiment Meter overlaid on the settlement price for the nearby futures contract (the front month) in Henry Hub Natural Gas physically delivered futures (NG).
Casual observation may suggest that bi-polar (event risk) periods are sometimes followed by important price moves. As a cautionary note, the concept of event risk is only that after an event, one of the two possible outcomes has clearly occurred, and that all of the market participants are now acting on this common knowledge. That said, the anticipated choice might have been between up or down, moving or staying still, high or low volatility, etc.
The sentiment state embedded in markets is inherently unobservable. Based on their observed actions -- prices, volumes and intra-day activity in futures and options markets – we hypothetically represent the risks which may be perceived by market participants. We do not claim any predictive value as we are only attempting to describe an unobservable risk-return distribution to inform discussions and analysis of marketplace risks.
The Market Sentiment Meter is available as a subscription, which may be ordered for any of the following products:
- CME S&P 500 Index E-Mini futures (ES) and options
- CBOT 10-Year Treasury Note futures (TYF) and options
- CME Euro/USD FX futures (EC) and options
- NYMEX WTI Crude Oil futures (CL) and options
- NYMEX Henry Hub Natural Gas futures (NG) and options
- COMEX Gold futures (GC) and options
- CBOT Soybean futures (S) and options
- CBOT Corn futures (C) and options
The subscription includes:
- Daily updates
- Full history from January 2012
- Curated Data File Package (CSV)
The Curated Data Files contain a wide variety of metrics, including futures settlement prices, futures and options volumes, a representative proxy for implied volatility for options, and many other derived series, as well as our market state classifier, which may be:
- Balanced
- Complacent
- Anxious
- Bi-polar (event risk).
Application notes and research papers will be made available to assist the subscriber as they are prepared and published.
Subscription files are provided as Comma Separated Values (CSV).
Application notes and R&D papers will be made available either as a downloadable PDF or through a web page, to be determined.
Curated Data File Package (CSV) per product ranges from 6 MB to 10 MB. This depends on the number of zeros in the file, which are represented by “0”, as opposed to the standard 9-digit precision.
There is a Curated Data File for each product which is updated after each trading day. There are currently eight products available: equities, treasuries, euro FX, gold, oil, natural gas, corn and soybeans.
The files are updated after the close of each business day, as soon as the preliminary end-of-day settlement files (P files) have been published by CME Group and made available to 1QBit.
You can always download the most recently updated files from CME DataMine. The updated files will normally be available within four hours of their publication by CME Group. Typically, the files will be available between 2 a.m. and 5 a.m. Central Time (CT). However, from time to time, delays may occur.
The CSV files are not compressed.
Sample files will be available with details available in the future.
Time series in the Curated Data File starts on January 3, 2012, the first futures and options trading day of 2012.
All price and volume data comes from the End-of-Day (EOD) settlement files published by CME Group and offered for purchase by CME DataMine.
The settlement price will always be the price published by CME Group.
In order to keep the time series for all of the products in exact alignment, the following special cases were handled as follows:
Good Friday
In recent years, no CME Group markets have been opened on Good Friday. In 2010, 2012 and 2015 however, the Equities, Rates and FX products were allowed to open on Thursday evening with Friday’s trade date, and allowed to trade overnight until 8 a.m. on Friday, after which the markets were closed and the trades booked on the Friday. The volume in all cases was small in comparison to that of nearby days. The Curated Data Files do not include any Good Friday data.
National Day of Mourning for former U.S. President George H. W. Bush (December 5, 2018)
There was no trading at all for interest rate products on December 5. CME Group published end-of-day settlement prices for December 5 that were identical to the prices reported for December 4. In equities, the markets were closed from 8:30 a.m. CT onward on December 5, but were open overnight, which made it possible for a regular settlement price to be published. All other markets remained open for their usually scheduled hours. The Curated Data Files contain the following data for interest rate futures and options:
- Settlement prices published by CME Group
- Total volume published by CME Group, which consisted of PNT (privately negotiated trades) that were cleared through CME Clearing. These PNT trades did not show up in high and low prices.
- High and low prices interpolated from the previous day, based on the percentage spread. Our method keeps the time series for all the MSM products based on exactly the same days. It also ensures that time-dependent calculations using raw data in the CSV file will match the same calculations done using the processed data in the CSV file.
In most futures products, volume and open interest is largest in the contract with the nearest expiry date. However, as the expiry date draws nearer, volume and open interest move to the next available expiry. This is referred to as the roll and can be spread over many days.
The Market Sentiment Meter defines a nearby futures contract and second futures contract. The nearby contract is usually exactly that, i.e. the futures contract with the closest expiry and the greatest volume. Each day, however, the MSM program compares the volume in the nearby contract with the volume in all subsequent expiries. When the volume in a later contract surpasses the volume in the nearby contract, the definition of the nearby futures contract is updated to be the new contract with the largest volume. The definition does not move back, even if the volume in the expiring contract temporarily exceeds the volume in the new nearby.
When the nearby futures contract is advanced to a later expiry, the second futures contract also advances.
For contracts such as Corn, which trades in March, May, July, September and December, the next expiry may be more than a month away. There are also contracts, such as Gold, that trade the nearest calendar months in addition to the standard months. The roll logic is driven by volume and does not attempt to select the expiry that “ought” to be next.
In order to keep day-to-day ratio data consistently defined across a roll, the Curated Data File reports the previous nearby reference price. This is the settlement price on the previous day for the contract being reported as the nearby contract.
For example, in CME Euro/USD FX futures (EC), the 2016 the Market Sentiment Meter’s nearby roll, from the December 2016 ECZ16 contract to the March 2017 ECH17 contract, took place on December 16. The second futures contract advanced from March to June on the same day.
- On December 15, the nearby contract was ECZ16, and the previous nearby reference price was $1.05605, the settlement price for ECZ16 on December 14
- On December 16, the nearby contract was ECH17, and the previous nearby reference price was $1.04715, the settlement price for ECZ17 on December 16
The return in the nearby contract is always computed from the previous nearby reference price.
Blank price data can be present for several reasons.
For example, if there was no volume traded in the second futures contract, there will be no high or low price to report. Bids and asks that do not trade are not used in the MSM calculations.
In some cases, there may be volume traded in a way that does not establish a high or low price, for example:
- Volume from trade-at-settlement orders
- Privately negotiated trades that are cleared by CME Group without price reporting
This situation occurs most frequently in 10 Year Treasury Note futures, which trade for March, June, September and December. When open interest is rolling from (say) March to June, there is typically not much activity in the September contract.
CME Group calculates a settlement price for all listed contracts, even if there is no trading on any given day. It is not uncommon for contracts with distant expiry dates to slowly accumulate open interest over many low-volume (and no-volume) days.
The Curated Data File contains a variety of smoothed time series. Our research has indicated that comparing short-term smoothed metrics to long-term smoothed metrics can lead to very useful insights into how market risk perceptions are evolving.
Smoothing is exponential. For example:
(today’s smoothed IVOL) = k * (today's IVOL) + ( k-1 ) * (yesterday's smoothed IVOL),
where k = 1/(number of smoothing days).
For short-term smoothed series, the number of smoothing days is 30 days.
For long-term smoothed series, the number of smoothing days is 200 days.
The number of days is configurable by product and we are continuing to conduct research related to the most appropriate smoothing processes.
We prefer an exponential smoothing process to a moving average window process. Exponential smoothing values recent data more highly than older data. In a moving average window, the data points within the time window are all considered equal, and we strongly believe that market participants do not process information in this manner. With a moving average window method, if a large movement occurs and then is reversed, the large temporary movement would retain the same impact even as it fades into history. With exponential smoothing, the large temporary movement loses influence every day.
All time series in the Curated Data File start on January 3, 2012, the first futures and options trading day of 2012. However, the initial values of the smoothed time series are based on data extending back to January 4, 2010.
Volume data reported in the Curated Data Files is the total daily volume reported by CME Group. This includes:
- CME Globex volume,
- Floor volume (where it exists)
- Exchange for Related Position (EFRP) volume
- Privately Negotiated Trades (PNT) cleared through CME Clearing
- Other volume subcategories designated by CME Group (these are typically quite small)
An EFRP can be an exchange for physical (EFP), e.g. from financially-settled futures to physical futures such as CL, NG, etc., an exchange of futures for risk (EFR), or an exchange of options for options (EOO). For additional detail on EFRP transactions in a specific product, consult the relevant sections of the Exchange Rule Book.
Historical volatility within the Market Sentiment Meter uses exponential smoothing as described above. For volatility, a weighted historical standard deviation is calculated from a Daily Variance Proxy, defined as the square of the percent change in price. The daily variance proxy is weighted exponentially, so that more recent price movements contribute more to this historically weighted standard deviation. This method mimics the traditional definition of volatility as the standard deviation of the distribution of percent price movements (as it is in the Black-Scholes model).
The Market Sentiment Meter is influenced by differences between the forward-looking volatility estimates seen in options prices, and the backward-looking volatility estimates made from the settlement prices in the underlying futures contracts.
The historical standard deviation is annualized so that it can be compared to other volatilities, most notably the implied volatilities published by CME Group.
While our MSM metrics process uses exponentially smoothed time series data, for ease of user comparisons and for use in momentum trading models, we also provide some pre-calculated moving averages. Each moving price average is the uniform windowed average of today’s settlement price and the settlement prices from prior days.
For example, the 20-day moving average is computed from today’s settlement price and the settlement prices from 19 prior days. The average is given to nine decimal places, regardless of the price ticking.
The Curated Data Files begin on January 3, 2012. The moving price averages, peak prices and other time-dependent data have been initialized with values based on settlement files prior to that date.
The moving price averages are calculated for the nearby futures contract settlement price. The 200-day moving price average will therefore contain one or more contract rolls. Even the 20-day moving average will contain a roll day in some contracts. Although there may be a small jump in the price when moving from expiry to the next, it is assumed that the averaging will give greater emphasis to the much larger number of non-roll days. That said, the interpretation of a 60-day moving price average in Crude Oil futures (which roll monthly) will have to be different from the interpretation of a 60-day moving price average in 10-Year Treasury Note futures, which roll quarterly.
All time series in the Curated Data File start on January 3, 2012, the first futures and options trading day of 2012. However, the initial values of the moving price averages are based on data extending back 20, 60 and 200 trading days into 2011.
The risk-return probability distribution is a proprietary process using a mixture distribution method. See our related research papers for more in-depth explanations. We report the standard parameters for the MSM risk-return probability distribution, including mean, median, first mode, second mode if any, standard deviation, skewness, and kurtosis.
The probabilities are calculated using today's risk-return probability distribution.
For example, to calculate the probability of reaching 20% above today’s 60-day average in the coming year: The price value for 20% above the 60-day moving average is expressed as a return relative to the today's settlement price and the distribution used to calculate the probability of this return being exceeded.
The target return is used as the left-hand side of a semi-infinite interval, and the probability calculated as the area under the tail of the distribution.
CsvHeaderName |
CsvHeaderLongName |
Definition |
Typical Value |
|---|---|---|---|
TRADEDATE |
Trade Date |
Business date for the settlement price and other data reported on this row. Expressed as an eight-digit integer in YYYYMMDD format (ISO 8601). |
20190731 |
DATA_SOURCE |
Data Source |
Source or citation information to be included on charts or tables using the data set. |
CME DataMine - Market Sentiment Meter powered by 1QBit |
EODDESC |
EOD Description |
Description of the underlying futures product as included in CME DataMine End of Day (EOD) file documentation. |
10-YR NOTE FUTURES |
CHART_TITLE |
Chart Title |
Description of the underlying futures product for inclusion in charts or tables using the data set. |
CBOT US Treasury 10-Year Note Futures |
YYYY |
Year |
YEAR of the business date, as an integer |
2019 |
MM |
Month |
MONTH of the business date, as an integer |
7 |
DD |
Day |
DAY of the business date, as an integer |
31 |
DATECODE_EXCEL |
Excel Date Code |
The five-digit Excel datacode for the Trade Date. |
43677 |
DATE_LABEL |
Date Label MMDDYYYY |
The Trade Date expressed in MM/DD/YYYY format. |
7/31/2019 |
F_PROD_CODE |
Futures Product Code |
Product code used by CME DataMine for the futures contract, in upper case |
TYF |
O_PROD_CODE |
Options Product Code |
Product code used by CME DataMine for the options contract being used in the model on this day. In most cases, the options code does not change through time; however, there is an exception for the option used for the Euro/USD FX (USD per EUR). The original option code future was ZC from 2012 to 2017, but EUU afterwards, after a shift in the product option type. This field always shows the option that was in use on the corresponding Trade Date. |
TC |
PRICE_SETTLE_ |
Most Active Futures Settlement Price |
The futures contract with the largest daily volume. Usually the most active contract is the nearby contract. When trading "rolls" from one expiry to the next, the actual nearby future is no longer the most active contract and our analysis shifts with the "roll". Once a new "most active" contract has been established, the curated data does not move backwards. |
127.421875 |
PRICE_HIGH_ACTIVE |
Most Active Futures High Price |
CME Globex High price as published by CME Group in the EOD settlement P (Preliminary) File for the most active futures contract. |
127.703125 |
PRICE_LOW_ACTIVE |
Most Active Futures Low Price |
CME Globex Low price as published by CME Group in the EOD settlement P (Preliminary) File for the most active futures contract. |
127.015625 |
YYYY_ACTIVE |
Most Active Futures Contract Year |
The year of the delivery month that defines the most active futures contract. Given as an integer. |
2019 |
MM_ACTIVE |
Most Active Futures Contract Month |
The delivery month that defines the most active futures contract, given as an integer. |
9 |
F_VOLUME_ACTIVE |
Most Active Futures Contract Volume |
Total volume traded and settled on the business day in the most active futures contract. Includes CME Globex volume, floor volume (where it exists), and EFRP (exchange for a related position). Total volume also includes PNT (privately negotiated trades) that are cleared through CME Clearing. |
2403170 |
PRICE_SETTLE_NEXT |
Next Futures Settlement Price |
The settlement price of the next futures contract after the most actively traded futures contract. |
127.890625 |
PRICE_HIGH_NEXT |
Next Futures High Price |
CME Globex High price as published by CME Group in the EOD settlement P (Preliminary) File for the next futures contract after the most active. |
128.140625 |
PRICE_LOW_NEXT |
Next Futures Low Price |
CME Globex Low price as published by CME Group in the EOD settlement P (Preliminary) File for the next futures contract after the most active. |
127.5 |
YYYY_NEXT |
Next Futures Contract Year |
The year of the delivery month that defines the next futures contract after the most active. Given as an integer. |
2019 |
MM_NEXT |
Next Futures Contract Month |
The delivery month that defines the next futures contract after the most active, given as an integer. |
12 |
F_VOLUME_NEXT |
Next Futures Contract Volume |
Total volume traded and settled on the business day in the next futures contract after the most active. Includes CME Globex volume, floor volume (where it exists), and EFRP (exchange for a related position). Total volume also includes PNT (privately negotiated trades) that are cleared through CME Clearing. |
19066 |
F_VOLUME |
Total Futures Volume |
Total futures volume as reported by CME Group for all of the futures contracts for this product. |
2422236 |
IMPLIED_VOL |
Representative Implied Volatility |
Representative implied volatility (IVOL) is chosen from the values published by CME Group using the following criteria: furthest expiry with a daily volume greater than 10 lots and a reported delta between 0.45 and 0.55. Of these, the contract with the largest traded volume is chosen, which may be a put or a call. Please note that the MSM intentionally has avoided the use of options contracts that do not trade on a given day even though the exchange is required to publish a settlement price. |
0.0384195 |
PUT_VOLUME |
Put Option Volume |
Total put options volume as reported by CME Group for all put options on the given product. |
188522 |
CALL_VOLUME |
Call Option Volume |
Total call options volume as reported by CME Group for all call options on the given product. |
156040 |
OPTIONS_VOLUME |
Total Option Volume |
Total options volume as reported by CME Group. This is the sum of the total put and total call volumes on the given product. |
344562 |
PUT_OI |
Put Option Open Interest |
Total put options open interest as reported by CME Group on the given product. |
2028681 |
CALL_OI |
Call Option Open Interest |
Total call options open interest as reported by CME Group on the given product. |
1214521 |
O_OI |
Total Option Open Interest |
Total options open interest as reported by CME Group. This is the sum of the total put and total call options open interest on the given product. |
3243202 |
CURRENT_PRICE_ |
Most Active Futures Current Day Reference Price |
Settlement price for today's most active futures contract taken from today's Trade Date. This is a duplicate of data provided earlier in a preceding column and included here for ease of use. |
127.421875 |
PREVIOUS_PRICE_ |
Most Active Futures Previous Day Reference Price |
Settlement price for today's most active futures contract taken from the previous trading day. |
127.34375 |
PRICE_PCT_CHG |
Daily Percent Change in Price using log differences |
The daily percentage change is calculated from today’s price and the previous day's price for the same contract as shown in the preceding two columns. The calculation is the difference in the natural logs, so that for analytical purposes there is symmetry in the calculations for up and down days. |
0.00061331 |
EXCESS_RETURN_ |
Excess Return Index (not including return on cash) |
The simple excess return index is calculated without including an estimated risk-free return). Hence, the excess return index does not include any interest that might have been earned in the margin account or by other assets backing the futures position. The excess return index is set to 100 on the Curated Data Start Date of January 3, 2012. For later days, it is calculated from the daily returns, so that it always applies to the most active futures contract (which changes across the rolls). |
111.637441 |
IMPLIED_VOL_ST |
Short-Term Smoothed Implied Volatility |
Smoothing is exponential, i.e. ( today's smoothed IVOL) = k * (today's IVOL) + ( 1-k ) * (yesterday's SMOOTHED IVOL), where k = 1/(short term days). Short-term days are set to 30. |
0.0401246 |
IMPLIED_VOL_LT |
Long-Term Smoothed Implied Volatility |
Smoothing is exponential, i.e. ( today's smoothed IVOL) = k * (today's IVOL) + ( 1-k ) * (yesterday's SMOOTHED IVOL), where k = 1/(long term days). Long-term days are set to 200. |
0.03905877 |
DAILY_VARIANCE |
Daily Variance Proxy |
The daily variance proxy is the square of the daily percent change in price. |
3.7615E-07 |
HISTORICAL_STD_ST |
Short-Term Smoothed Historical Standard Deviation |
The short-term smoothed historical standard deviation is computed by exponential smoothing of the daily variance proxy with a time constant of 30 days, then taking the square root, and then annualizing the value. |
0.03670488 |
HISTORICAL_STD_LT |
Long-Term Smoothed Historical Standard Deviation |
The long-term smoothed historical standard deviation is computed by exponential smoothing of the daily variance proxy with a time constant of 200 days, then taking the square root, and then annualizing the value. |
0.03734958 |
RATIO_STD_ST_LT |
Ratio of Short-Term to Long-Term Smoothed Standard Deviation |
The ratio of the short-term smoothed historical standard deviation to the long-term smoothed historical standard deviation, as defined above. |
0.98273881 |
RATIO_STD_ST_ |
Ratio of Short-Term HISTORICAL STD DEV to Current Implied Volatility |
The ratio of the short-term smoothed historical standard deviation to the implied volatility of the underlying futures product, computed from the most distant but still actively traded near the money options (See representative implied volatility above). |
0.95537118 |
RATIO_HIGH_LOW_PCT |
High Price to Low Price Ratio as Percent Spread |
High price minus the low price, divided by the low price. For the most active futures contract. Computed as a difference of logs. |
0.00539812 |
HIGH_LOW_PCT_ST |
Short-Term Smoothed High-Low Percentage Spread |
Same as other short term smoothed data. Exponentially smoothed with a time constant of 30 days. |
0.00394707 |
HIGH_LOW_PCT_LT |
Long-Term Smoothed High-Low Percentage Spread |
Same as other long term smoothed data. Exponentially smoothed with a time constant of 200 days. |
0.00371019 |
RATIO_HIGH_LOW_ST_LT |
Ratio of Short-Term Smoothed to Long-Term Smoothed High-Low Percentage Spread |
The ratio of the short-term smoothed high-low spread to the long-term smoothed high-low spread. |
1.06384468 |
PUT_VOLUME_ST |
Short-Term Smoothed Put Option Volume |
Same as other short term smoothed data. Exponentially smoothed with a time constant of 30 days. |
252056.728 |
PUT_VOLUME_LT |
Long-Term Smoothed Put Option Volume |
Same as other long term smoothed data. Exponentially smoothed with a time constant of 200 days. |
236591.061 |
RATIO_PUT_ |
Ratio of Short-Term Smoothed to Long-Term Smoothed Put Option Volume |
The ratio of the short-term smoothed put option volume to the long-term smoothed put option volume. |
1.06536877 |
CALL_VOLUME_ST |
Short-Term Smoothed Call Option Volume |
Same as other short term smoothed data. Exponentially smoothed with a time constant of 30 days. |
213453.891 |
CALL_VOLUME_LT |
Long-Term Smoothed Call Option Volume |
Same as other long term smoothed data. Exponentially smoothed with a time constant of 200 days. |
246498.25 |
RATIO_CALL_ |
Ratio of Short-Term to Long-Term Smoothed Call Option Volume |
The ratio of the short-term smoothed call option volume to the long-term smoothed call option volume. |
0.86594485 |
RATIO_PUT_CALL_ |
Ratio of Short-Term Smoothed Put Option Volume to Short Term Smoothed Call Option Volume |
The ratio of Short-Term Smoothed Put Option Volume to the Short-Term Smoothed Call Option Volume. |
1.1808486 |
RATIO_PUT_CALL_ |
Ratio of Long-Term Smoothed Put Option Volume to Long-Term Smoothed Call Option Volume |
The ratio of Long-Term Smoothed Put Option Volume to the Long-Term Smoothed Call Option Volume. |
0.95980828 |
PCT_DIF_PUT_CALL_ST_LT_RATIO |
Percentage Difference Short-Term to Long-Term Ratio of Put to Call Volume |
The percentage difference between the short-term and long-term ratios for put to call option volume. |
0.22104032 |
MOMENTUM_ST |
Short-Term Smoothed Return Momentum Annualized |
The single-day return momentum is defined as the percent change in price, computed as a difference of natural logs. The short-term smoothed return momentum is the exponentially-smoothed average of these percent changes, with a time constant of 30 days. |
0.0535291 |
MOMENTUM_LT |
Long-Term Smoothed Return Momentum Annualized |
The single-day return momentum is defined as the percent change in price, computed as a difference of natural logs. The long-term smoothed return momentum is the exponentially-smoothed average of these percent changes, with a time constant of 200 days. |
0.04251305 |
RATIO_MOMENTUM_ST_LT |
Ratio of Short-Term to Long-Term Smoothed Return Momentum |
Ratio of short-term to long-term return momentum. |
1.25912144 |
RATIO_MOMENTUM_TO_STD_ST |
Ratio of Short-Term Return Momentum to Short-Term Standard Deviation |
Ratio of short-term momentum to short-term historical standard deviation. This is a proxy for a signal to noise ratio, such as an information ratio or Sharpe Ratio. |
1.45836447 |
RATIO_MOMENTUM_TO_STD_LT |
Ratio of Long-Term Return Momentum to Long-Term Standard Deviation |
Ratio of long-term momentum to long-term historical standard deviation. This is a proxy for a signal to noise ratio, such as an information ratio or Sharpe Ratio. |
1.13824713 |
PRICE_20D_MA |
20-Day Price Moving Average |
Moving average of most active settlement prices for last 20 trading days. Please note that moving averages equally weight each day, while exponential smoothing gives more weight to more recent observations. For analytical purposes, we use exponential smoothing. Moving averages are provided for comparison purposes. |
127.392969 |
PRICE_60D_MA |
60-Day Price Moving Average |
Moving average of most active settlement prices for last 60 trading days. Please note that moving averages equally weight each day, while exponential smoothing gives more weight to more recent observations. For analytical purposes, we use exponential smoothing. Moving averages are provided for comparison purposes. |
126.614583 |
PRICE_200D_MA |
200-Day Price Moving Average |
Moving average of most active settlement prices for last 200 trading days. Please note that moving averages equally weight each day, while exponential smoothing gives more weight to more recent observations. For analytical purposes, we use exponential smoothing. Moving averages are provided for comparison purposes. |
122.968516 |
PCT_DIF_CURRENT_ |
Percentage Difference Current Price to 200-Day Moving Average |
Percentage difference between the current price and the 200-day moving average. |
0.03621544 |
PCT_DIF_20D_200D_ |
Percentage Difference 20-Day Price Moving Average to 200-Day Price Moving Average |
Percentage difference between the 20-day and the 200-day moving average. |
0.03598037 |
PEAK_PRICE |
Peak price from Jan-2012 to current |
Peak price since the inception of this data set on 3 January 2012. |
135.265625 |
PEAK_200D_PRICE |
Peak Price of Nearby Futures in Last 200 Days |
Peak price occurring in the previous 200 days. |
128.25 |
20PCT_BELOW_PEAK_200D |
Price level 20 pct below peak price in last 200-business days |
Price level that would be 20 percent below the peak price of the last 200 days. |
102.6 |
20PCT_ABOVE_ |
Price level 20 pct above 60-business day moving average |
Price level that would be 20 percent above the moving price average for the last 60 days. |
151.9375 |
20PCT_BELOW_ |
Price level 20 pct Below 60-day moving average of price level |
Price level that would be 20 percent below the moving price average for the last 60 days. |
101.291667 |
MIX_PROB_20PCT_ |
Probability of Rising Above 20 pct above 60-business day moving average |
Based on our hypothetical mixture risk-return distribution, we calculate the probability of the price rising above 20 percent above the 60-day moving average. |
6.4892E-08 |
MIX_PROB_20PCT_ |
Probability of Falling Below 20 pct below 60-business day moving average |
Based on our hypothetical mixture risk-return distribution, we calculate the probability of the price falling below 20 percent below the 60-day moving average. |
8.6718E-09 |
MIX_MEAN |
Mean of Mixture Probability Distribution |
Mean of our hypothetical mixture risk-return distribution is always set to zero by definition. |
0 |
MIX_MEDIAN |
Median of Mixture Probability Distribution |
Median of our hypothetical mixture risk-return distribution, which may differ from zero when skewness is present in the distribution. |
-0.01 |
MIX_MODE_1 |
Primary Mode of Mixture Probability Distribution |
Primary mode of our hypothetical mixture risk-return distribution, which may differ from zero when skewness is present in the distribution. |
-0.02 |
MIX_MODE_2 |
Secondary Mode of Mixture Probability Distribution |
Secondary mode of our hypothetical mixture risk-return distribution, which will occur only when a bi-modal distribution is present. Otherwise this field is left blank. |
|
MIX_STD |
Standard Deviation of Mixture Distribution |
Standard deviation of our hypothetical mixture risk-return distribution. |
0.03635327 |
MIX_STD_LT |
Long-term Smoothed STD of Mixture Distribution |
Long-term smoothed standard deviation of the hypothetical mixture risk-return distribution. |
0.04002093 |
MIX_SKEW |
Skew of Mixture Probability Distribution |
Skewness of our hypothetical mixture risk-return distribution. |
0.2620422 |
MIX_KURTOSIS |
Kurtosis of Mixture Probability Distribution |
Kurtosis of our hypothetical mixture risk-return distribution. |
2.91840249 |
MIX_STATE |
State of Mixture Probability Distribution |
Sentiment state of the risk-return distribution may be classified as complacent, balanced, anxious, or conflicted (bi-modal when event risk is identified). |
Balanced |
MIX_COMPLACENT |
Complacent (1 or 0) |
If the sentiment state is complacent, the value is reported a 1, otherwise zero. This data field is provided for ease in charting when the risk-return distribution is in this specific state. |
0 |
MIX_BALANCED |
Balanced (1 or 0) |
If the sentiment state is balanced, the value is reported a 1, otherwise zero. This data field is provided for ease in charting when the risk-return distribution is in this specific state. |
1 |
MIX_ANXIOUS |
Anxious (1 or 0) |
If the sentiment state is anxious, the value is reported a 1, otherwise zero. This data field is provided for ease in charting when the risk-return distribution is in this specific state. |
0 |
MIX_CONFLICTED |
Bi-Modal (1 or 0) |
If the sentiment state is conflicted, the value is reported a 1, otherwise zero. This data field is provided for ease in charting when the risk-return distribution is in this specific state. |
0 |
MIX_MODALITY |
Single Mode or Bi-Modal |
Reports whether the risk-return distribution is a single-mode or bi-modal distribution. |
Single Mode |
MIX_DISTANCE |
Distance Number of Bins between Modes if Bimodal |
If the risk-return distribution is bi-modal (Conflicted sentiment state), we measure the number of element bins between the modes as one measure of the extent of the bi-modality. Reported as an integer. For a single-mode distribution this field is blank. |
|
MIX_INTENSITY |
Intensity Measurement Index of Height of Second Mode compared to Low Point of Valley in between modes. |
If the risk-return distribution is bi-modal (Conflicted sentiment state), we compute the ratio between the height of the second mode and the lowest value of the distribution between the two modes. For a single-mode distribution this field is blank. |
|
MIX_LOW_BIN |
Origin for Distribution |
The worst case element bin is minus 100% or -1. |
-1 |
MIX_BIN_SIZE |
Stepsize for Distribution |
The element bins have a width of 1% or 0.01. |
0.01 |
MIX_BINS |
Number of elements in the distribution vector |
We report 256 element bins, from -100% to +155% |
256 |
MIX_BIN_NEG_100 |
-1 |
Probability associated with each element bin for the discreet risk-return probability distribution. Probabilities sum to 100% or 1 over the whole risk-return distribution from -100% to +155%. Low volatility products will have many zeroes on both ends. High volatility products will have fewer zeroes. |
0 |
MIX_BIN_NEG_99 |
-0.99 |
Element bin probability. |
0 |
MIX_BIN_NEG_98 |
-0.98 |
Element bin probability. |
0 |
MIX_BIN_NEG_97 |
-0.97 |
Element bin probability. |
0 |
MIX_BIN_NEG_96 |
-0.96 |
Element bin probability. |
0 |
MIX_BIN_NEG_95 |
-0.95 |
Element bin probability. |
0 |
MIX_BIN_NEG_94 |
-0.94 |
Element bin probability. |
0 |
MIX_BIN_NEG_93 |
-0.93 |
Element bin probability. |
0 |
MIX_BIN_NEG_92 |
-0.92 |
Element bin probability. |
0 |
MIX_BIN_NEG_91 |
-0.91 |
Element bin probability. |
0 |
MIX_BIN_NEG_90 |
-0.9 |
Element bin probability. |
0 |
MIX_BIN_NEG_89 |
-0.89 |
Element bin probability. |
0 |
MIX_BIN_NEG_88 |
-0.88 |
Element bin probability. |
0 |
MIX_BIN_NEG_87 |
-0.87 |
Element bin probability. |
0 |
MIX_BIN_NEG_86 |
-0.86 |
Element bin probability. |
0 |
MIX_BIN_NEG_85 |
-0.85 |
Element bin probability. |
0 |
MIX_BIN_NEG_84 |
-0.84 |
Element bin probability. |
0 |
MIX_BIN_NEG_83 |
-0.83 |
Element bin probability. |
0 |
MIX_BIN_NEG_82 |
-0.82 |
Element bin probability. |
0 |
MIX_BIN_NEG_81 |
-0.81 |
Element bin probability. |
0 |
MIX_BIN_NEG_80 |
-0.8 |
Element bin probability. |
0 |
MIX_BIN_NEG_79 |
-0.79 |
Element bin probability. |
0 |
MIX_BIN_NEG_78 |
-0.78 |
Element bin probability. |
0 |
MIX_BIN_NEG_77 |
-0.77 |
Element bin probability. |
0 |
MIX_BIN_NEG_76 |
-0.76 |
Element bin probability. |
0 |
MIX_BIN_NEG_75 |
-0.75 |
Element bin probability. |
0 |
MIX_BIN_NEG_74 |
-0.74 |
Element bin probability. |
0 |
MIX_BIN_NEG_73 |
-0.73 |
Element bin probability. |
0 |
MIX_BIN_NEG_72 |
-0.72 |
Element bin probability. |
0 |
MIX_BIN_NEG_71 |
-0.71 |
Element bin probability. |
0 |
MIX_BIN_NEG_70 |
-0.7 |
Element bin probability. |
0 |
MIX_BIN_NEG_69 |
-0.69 |
Element bin probability. |
0 |
MIX_BIN_NEG_68 |
-0.68 |
Element bin probability. |
0 |
MIX_BIN_NEG_67 |
-0.67 |
Element bin probability. |
0 |
MIX_BIN_NEG_66 |
-0.66 |
Element bin probability. |
0 |
MIX_BIN_NEG_65 |
-0.65 |
Element bin probability. |
0 |
MIX_BIN_NEG_64 |
-0.64 |
Element bin probability. |
0 |
MIX_BIN_NEG_63 |
-0.63 |
Element bin probability. |
0 |
MIX_BIN_NEG_62 |
-0.62 |
Element bin probability. |
0 |
MIX_BIN_NEG_61 |
-0.61 |
Element bin probability. |
0 |
MIX_BIN_NEG_60 |
-0.6 |
Element bin probability. |
0 |
MIX_BIN_NEG_59 |
-0.59 |
Element bin probability. |
0 |
MIX_BIN_NEG_58 |
-0.58 |
Element bin probability. |
0 |
MIX_BIN_NEG_57 |
-0.57 |
Element bin probability. |
0 |
MIX_BIN_NEG_56 |
-0.56 |
Element bin probability. |
0 |
MIX_BIN_NEG_55 |
-0.55 |
Element bin probability. |
0 |
MIX_BIN_NEG_54 |
-0.54 |
Element bin probability. |
0 |
MIX_BIN_NEG_53 |
-0.53 |
Element bin probability. |
0 |
MIX_BIN_NEG_52 |
-0.52 |
Element bin probability. |
0 |
MIX_BIN_NEG_51 |
-0.51 |
Element bin probability. |
0 |
MIX_BIN_NEG_50 |
-0.5 |
Element bin probability. |
0 |
MIX_BIN_NEG_49 |
-0.49 |
Element bin probability. |
0 |
MIX_BIN_NEG_48 |
-0.48 |
Element bin probability. |
0 |
MIX_BIN_NEG_47 |
-0.47 |
Element bin probability. |
0 |
MIX_BIN_NEG_46 |
-0.46 |
Element bin probability. |
0 |
MIX_BIN_NEG_45 |
-0.45 |
Element bin probability. |
0 |
MIX_BIN_NEG_44 |
-0.44 |
Element bin probability. |
0 |
MIX_BIN_NEG_43 |
-0.43 |
Element bin probability. |
0 |
MIX_BIN_NEG_42 |
-0.42 |
Element bin probability. |
0 |
MIX_BIN_NEG_41 |
-0.41 |
Element bin probability. |
0 |
MIX_BIN_NEG_40 |
-0.4 |
Element bin probability. |
0 |
MIX_BIN_NEG_39 |
-0.39 |
Element bin probability. |
0 |
MIX_BIN_NEG_38 |
-0.38 |
Element bin probability. |
0 |
MIX_BIN_NEG_37 |
-0.37 |
Element bin probability. |
0 |
MIX_BIN_NEG_36 |
-0.36 |
Element bin probability. |
0 |
MIX_BIN_NEG_35 |
-0.35 |
Element bin probability. |
0 |
MIX_BIN_NEG_34 |
-0.34 |
Element bin probability. |
0 |
MIX_BIN_NEG_33 |
-0.33 |
Element bin probability. |
0 |
MIX_BIN_NEG_32 |
-0.32 |
Element bin probability. |
0 |
MIX_BIN_NEG_31 |
-0.31 |
Element bin probability. |
0 |
MIX_BIN_NEG_30 |
-0.3 |
Element bin probability. |
0 |
MIX_BIN_NEG_29 |
-0.29 |
Element bin probability. |
0 |
MIX_BIN_NEG_28 |
-0.28 |
Element bin probability. |
0 |
MIX_BIN_NEG_27 |
-0.27 |
Element bin probability. |
0 |
MIX_BIN_NEG_26 |
-0.26 |
Element bin probability. |
0 |
MIX_BIN_NEG_25 |
-0.25 |
Element bin probability. |
0 |
MIX_BIN_NEG_24 |
-0.24 |
Element bin probability. |
0 |
MIX_BIN_NEG_23 |
-0.23 |
Element bin probability. |
0 |
MIX_BIN_NEG_22 |
-0.22 |
Element bin probability. |
0 |
MIX_BIN_NEG_21 |
-0.21 |
Element bin probability. |
0 |
MIX_BIN_NEG_20 |
-0.2 |
Element bin probability. |
0.000001 |
MIX_BIN_NEG_19 |
-0.19 |
Element bin probability. |
0.000005 |
MIX_BIN_NEG_18 |
-0.18 |
Element bin probability. |
0.000021 |
MIX_BIN_NEG_17 |
-0.17 |
Element bin probability. |
0.000082 |
MIX_BIN_NEG_16 |
-0.16 |
Element bin probability. |
0.000292 |
MIX_BIN_NEG_15 |
-0.15 |
Element bin probability. |
0.000968 |
MIX_BIN_NEG_14 |
-0.14 |
Element bin probability. |
0.002983 |
MIX_BIN_NEG_13 |
-0.13 |
Element bin probability. |
0.008533 |
MIX_BIN_NEG_12 |
-0.12 |
Element bin probability. |
0.022671 |
MIX_BIN_NEG_11 |
-0.11 |
Element bin probability. |
0.056021 |
MIX_BIN_NEG_10 |
-0.1 |
Element bin probability. |
0.129387 |
MIX_BIN_NEG_09 |
-0.09 |
Element bin probability. |
0.283008 |
MIX_BIN_NEG_08 |
-0.08 |
Element bin probability. |
0.599353 |
MIX_BIN_NEG_07 |
-0.07 |
Element bin probability. |
1.247273 |
MIX_BIN_NEG_06 |
-0.06 |
Element bin probability. |
2.499117 |
MIX_BIN_NEG_05 |
-0.05 |
Element bin probability. |
4.565155 |
MIX_BIN_NEG_04 |
-0.04 |
Element bin probability. |
7.201409 |
MIX_BIN_NEG_03 |
-0.03 |
Element bin probability. |
9.554258 |
MIX_BIN_NEG_02 |
-0.02 |
Element bin probability. |
10.761779 |
MIX_BIN_NEG_01 |
-0.01 |
Element bin probability. |
10.742357 |
MIX_BIN_POS_00 |
0 |
Element bin probability. |
10.081583 |
MIX_BIN_POS_01 |
0.01 |
Element bin probability. |
9.25683 |
MIX_BIN_POS_02 |
0.02 |
Element bin probability. |
8.31102 |
MIX_BIN_POS_03 |
0.03 |
Element bin probability. |
7.137581 |
MIX_BIN_POS_04 |
0.04 |
Element bin probability. |
5.758253 |
MIX_BIN_POS_05 |
0.05 |
Element bin probability. |
4.327795 |
MIX_BIN_POS_06 |
0.06 |
Element bin probability. |
3.022312 |
MIX_BIN_POS_07 |
0.07 |
Element bin probability. |
1.959933 |
MIX_BIN_POS_08 |
0.08 |
Element bin probability. |
1.180115 |
MIX_BIN_POS_09 |
0.09 |
Element bin probability. |
0.659754 |
MIX_BIN_POS_10 |
0.1 |
Element bin probability. |
0.342463 |
MIX_BIN_POS_11 |
0.11 |
Element bin probability. |
0.165052 |
MIX_BIN_POS_12 |
0.12 |
Element bin probability. |
0.073858 |
MIX_BIN_POS_13 |
0.13 |
Element bin probability. |
0.030687 |
MIX_BIN_POS_14 |
0.14 |
Element bin probability. |
0.011838 |
MIX_BIN_POS_15 |
0.15 |
Element bin probability. |
0.00424 |
MIX_BIN_POS_16 |
0.16 |
Element bin probability. |
0.00141 |
MIX_BIN_POS_17 |
0.17 |
Element bin probability. |
0.000435 |
MIX_BIN_POS_18 |
0.18 |
Element bin probability. |
0.000125 |
MIX_BIN_POS_19 |
0.19 |
Element bin probability. |
0.000033 |
MIX_BIN_POS_20 |
0.2 |
Element bin probability. |
0.000008 |
MIX_BIN_POS_21 |
0.21 |
Element bin probability. |
0.000002 |
MIX_BIN_POS_22 |
0.22 |
Element bin probability. |
0 |
MIX_BIN_POS_23 |
0.23 |
Element bin probability. |
0 |
MIX_BIN_POS_24 |
0.24 |
Element bin probability. |
0 |
MIX_BIN_POS_25 |
0.25 |
Element bin probability. |
0 |
MIX_BIN_POS_26 |
0.26 |
Element bin probability. |
0 |
MIX_BIN_POS_27 |
0.27 |
Element bin probability. |
0 |
MIX_BIN_POS_28 |
0.28 |
Element bin probability. |
0 |
MIX_BIN_POS_29 |
0.29 |
Element bin probability. |
0 |
MIX_BIN_POS_30 |
0.3 |
Element bin probability. |
0 |
MIX_BIN_POS_31 |
0.31 |
Element bin probability. |
0 |
MIX_BIN_POS_32 |
0.32 |
Element bin probability. |
0 |
MIX_BIN_POS_33 |
0.33 |
Element bin probability. |
0 |
MIX_BIN_POS_34 |
0.34 |
Element bin probability. |
0 |
MIX_BIN_POS_35 |
0.35 |
Element bin probability. |
0 |
MIX_BIN_POS_36 |
0.36 |
Element bin probability. |
0 |
MIX_BIN_POS_37 |
0.37 |
Element bin probability. |
0 |
MIX_BIN_POS_38 |
0.38 |
Element bin probability. |
0 |
MIX_BIN_POS_39 |
0.39 |
Element bin probability. |
0 |
MIX_BIN_POS_40 |
0.4 |
Element bin probability. |
0 |
MIX_BIN_POS_41 |
0.41 |
Element bin probability. |
0 |
MIX_BIN_POS_42 |
0.42 |
Element bin probability. |
0 |
MIX_BIN_POS_43 |
0.43 |
Element bin probability. |
0 |
MIX_BIN_POS_44 |
0.44 |
Element bin probability. |
0 |
MIX_BIN_POS_45 |
0.45 |
Element bin probability. |
0 |
MIX_BIN_POS_46 |
0.46 |
Element bin probability. |
0 |
MIX_BIN_POS_47 |
0.47 |
Element bin probability. |
0 |
MIX_BIN_POS_48 |
0.48 |
Element bin probability. |
0 |
MIX_BIN_POS_49 |
0.49 |
Element bin probability. |
0 |
MIX_BIN_POS_50 |
0.5 |
Element bin probability. |
0 |
MIX_BIN_POS_51 |
0.51 |
Element bin probability. |
0 |
MIX_BIN_POS_52 |
0.52 |
Element bin probability. |
0 |
MIX_BIN_POS_53 |
0.53 |
Element bin probability. |
0 |
MIX_BIN_POS_54 |
0.54 |
Element bin probability. |
0 |
MIX_BIN_POS_55 |
0.55 |
Element bin probability. |
0 |
MIX_BIN_POS_56 |
0.56 |
Element bin probability. |
0 |
MIX_BIN_POS_57 |
0.57 |
Element bin probability. |
0 |
MIX_BIN_POS_58 |
0.58 |
Element bin probability. |
0 |
MIX_BIN_POS_59 |
0.59 |
Element bin probability. |
0 |
MIX_BIN_POS_60 |
0.6 |
Element bin probability. |
0 |
MIX_BIN_POS_61 |
0.61 |
Element bin probability. |
0 |
MIX_BIN_POS_62 |
0.62 |
Element bin probability. |
0 |
MIX_BIN_POS_63 |
0.63 |
Element bin probability. |
0 |
MIX_BIN_POS_64 |
0.64 |
Element bin probability. |
0 |
MIX_BIN_POS_65 |
0.65 |
Element bin probability. |
0 |
MIX_BIN_POS_66 |
0.66 |
Element bin probability. |
0 |
MIX_BIN_POS_67 |
0.67 |
Element bin probability. |
0 |
MIX_BIN_POS_68 |
0.68 |
Element bin probability. |
0 |
MIX_BIN_POS_69 |
0.69 |
Element bin probability. |
0 |
MIX_BIN_POS_70 |
0.7 |
Element bin probability. |
0 |
MIX_BIN_POS_71 |
0.71 |
Element bin probability. |
0 |
MIX_BIN_POS_72 |
0.72 |
Element bin probability. |
0 |
MIX_BIN_POS_73 |
0.73 |
Element bin probability. |
0 |
MIX_BIN_POS_74 |
0.74 |
Element bin probability. |
0 |
MIX_BIN_POS_75 |
0.75 |
Element bin probability. |
0 |
MIX_BIN_POS_76 |
0.76 |
Element bin probability. |
0 |
MIX_BIN_POS_77 |
0.77 |
Element bin probability. |
0 |
MIX_BIN_POS_78 |
0.78 |
Element bin probability. |
0 |
MIX_BIN_POS_79 |
0.79 |
Element bin probability. |
0 |
MIX_BIN_POS_80 |
0.8 |
Element bin probability. |
0 |
MIX_BIN_POS_81 |
0.81 |
Element bin probability. |
0 |
MIX_BIN_POS_82 |
0.82 |
Element bin probability. |
0 |
MIX_BIN_POS_83 |
0.83 |
Element bin probability. |
0 |
MIX_BIN_POS_84 |
0.84 |
Element bin probability. |
0 |
MIX_BIN_POS_85 |
0.85 |
Element bin probability. |
0 |
MIX_BIN_POS_86 |
0.86 |
Element bin probability. |
0 |
MIX_BIN_POS_87 |
0.87 |
Element bin probability. |
0 |
MIX_BIN_POS_88 |
0.88 |
Element bin probability. |
0 |
MIX_BIN_POS_89 |
0.89 |
Element bin probability. |
0 |
MIX_BIN_POS_90 |
0.9 |
Element bin probability. |
0 |
MIX_BIN_POS_91 |
0.91 |
Element bin probability. |
0 |
MIX_BIN_POS_92 |
0.92 |
Element bin probability. |
0 |
MIX_BIN_POS_93 |
0.93 |
Element bin probability. |
0 |
MIX_BIN_POS_94 |
0.94 |
Element bin probability. |
0 |
MIX_BIN_POS_95 |
0.95 |
Element bin probability. |
0 |
MIX_BIN_POS_96 |
0.96 |
Element bin probability. |
0 |
MIX_BIN_POS_97 |
0.97 |
Element bin probability. |
0 |
MIX_BIN_POS_98 |
0.98 |
Element bin probability. |
0 |
MIX_BIN_POS_99 |
0.99 |
Element bin probability. |
0 |
MIX_BIN_POS_100 |
1 |
Element bin probability. |
0 |
MIX_BIN_POS_101 |
1.01 |
Element bin probability. |
0 |
MIX_BIN_POS_102 |
1.02 |
Element bin probability. |
0 |
MIX_BIN_POS_103 |
1.03 |
Element bin probability. |
0 |
MIX_BIN_POS_104 |
1.04 |
Element bin probability. |
0 |
MIX_BIN_POS_105 |
1.05 |
Element bin probability. |
0 |
MIX_BIN_POS_106 |
1.06 |
Element bin probability. |
0 |
MIX_BIN_POS_107 |
1.07 |
Element bin probability. |
0 |
MIX_BIN_POS_108 |
1.08 |
Element bin probability. |
0 |
MIX_BIN_POS_109 |
1.09 |
Element bin probability. |
0 |
MIX_BIN_POS_110 |
1.1 |
Element bin probability. |
0 |
MIX_BIN_POS_111 |
1.11 |
Element bin probability. |
0 |
MIX_BIN_POS_112 |
1.12 |
Element bin probability. |
0 |
MIX_BIN_POS_113 |
1.13 |
Element bin probability. |
0 |
MIX_BIN_POS_114 |
1.14 |
Element bin probability. |
0 |
MIX_BIN_POS_115 |
1.15 |
Element bin probability. |
0 |
MIX_BIN_POS_116 |
1.16 |
Element bin probability. |
0 |
MIX_BIN_POS_117 |
1.17 |
Element bin probability. |
0 |
MIX_BIN_POS_118 |
1.18 |
Element bin probability. |
0 |
MIX_BIN_POS_119 |
1.19 |
Element bin probability. |
0 |
MIX_BIN_POS_120 |
1.2 |
Element bin probability. |
0 |
MIX_BIN_POS_121 |
1.21 |
Element bin probability. |
0 |
MIX_BIN_POS_122 |
1.22 |
Element bin probability. |
0 |
MIX_BIN_POS_123 |
1.23 |
Element bin probability. |
0 |
MIX_BIN_POS_124 |
1.24 |
Element bin probability. |
0 |
MIX_BIN_POS_125 |
1.25 |
Element bin probability. |
0 |
MIX_BIN_POS_126 |
1.26 |
Element bin probability. |
0 |
MIX_BIN_POS_127 |
1.27 |
Element bin probability. |
0 |
MIX_BIN_POS_128 |
1.28 |
Element bin probability. |
0 |
MIX_BIN_POS_129 |
1.29 |
Element bin probability. |
0 |
MIX_BIN_POS_130 |
1.3 |
Element bin probability. |
0 |
MIX_BIN_POS_131 |
1.31 |
Element bin probability. |
0 |
MIX_BIN_POS_132 |
1.32 |
Element bin probability. |
0 |
MIX_BIN_POS_133 |
1.33 |
Element bin probability. |
0 |
MIX_BIN_POS_134 |
1.34 |
Element bin probability. |
0 |
MIX_BIN_POS_135 |
1.35 |
Element bin probability. |
0 |
MIX_BIN_POS_136 |
1.36 |
Element bin probability. |
0 |
MIX_BIN_POS_137 |
1.37 |
Element bin probability. |
0 |
MIX_BIN_POS_138 |
1.38 |
Element bin probability. |
0 |
MIX_BIN_POS_139 |
1.39 |
Element bin probability. |
0 |
MIX_BIN_POS_140 |
1.4 |
Element bin probability. |
0 |
MIX_BIN_POS_141 |
1.41 |
Element bin probability. |
0 |
MIX_BIN_POS_142 |
1.42 |
Element bin probability. |
0 |
MIX_BIN_POS_143 |
1.43 |
Element bin probability. |
0 |
MIX_BIN_POS_144 |
1.44 |
Element bin probability. |
0 |
MIX_BIN_POS_145 |
1.45 |
Element bin probability. |
0 |
MIX_BIN_POS_146 |
1.46 |
Element bin probability. |
0 |
MIX_BIN_POS_147 |
1.47 |
Element bin probability. |
0 |
MIX_BIN_POS_148 |
1.48 |
Element bin probability. |
0 |
MIX_BIN_POS_149 |
1.49 |
Element bin probability. |
0 |
MIX_BIN_POS_150 |
1.5 |
Element bin probability. |
0 |
MIX_BIN_POS_151 |
1.51 |
Element bin probability. |
0 |
MIX_BIN_POS_152 |
1.52 |
Element bin probability. |
0 |
MIX_BIN_POS_153 |
1.53 |
Element bin probability. |
0 |
MIX_BIN_POS_154 |
1.54 |
Element bin probability. |
0 |
MIX_BIN_POS_155 |
1.55 |
Element bin probability. |
0 |