
QuikVol Option Volatility Data is powered by QuikStrike, a benchmark pricing and analysis platform.
- Who is Bantix?
- What type of data does Bantix QuikVol provide?
- Do you provide all expirations for all products? Even deferred contracts?
- Can I see the data in chart format in CME DataMine? Elsewhere?
- Is strike level derived data available in CME DataMine? Elsewhere?
- What type or level of downloads can I receive?
- What is the data source for this derived volatility data?
- How is data calculated?
- How do you handle expirations with little or no open interest? Settlement data?
- How do you handle limit up and down settlement days?
- Can I get option settlement data, volume and open interest as part of this download?
- Can I get future settlement data, volume and open interest as part of this download?
- What is the file format of the Bantix QuikVol data?
- What is the average daily file size?
- How many files are available per day?
- What is the delivery frequency of the data?
- What time is delivery time of the data each day?
- Are files compressed?
- How far back historically is data available?
- Will Bitcoin (BRR or BTC) realized volatility be available anytime soon?
- What pricing models are used to initially create the implied volatility calculations?
- What asset classes and products are included?
- How do I use the curve coefficient data to calculate the strike level volatility?
- Can I see a data sample for the implied option volatility curves? Column list and explanation?
- Can I see a data sample for the realized futures volatility data? Column list and explanation?
- Disclaimer
Bantix is a Chicago-area-based software development firm specializing in the delivery of web-based tools. QuikStrike, their flagship options pricing and analysis product, has been available and in production since 2004. A free introductory version of QuikStrike is available on the CME Group website. More advanced versions are available as part of CME Direct, as well as the more advanced Professional and Enterprise subscription editions.
Bantix provides market implied option volatility curves and realized futures volatility data.
The following fourth order volatility curve types for listed and constant maturity expirations are available:
- Strike
- Delta
- Moneyness1 – normalizes x-axis by days to expiration (DTE)
- LOG(K/F) / SQRT(DTE) where K=strike and F=future
- Normal Model: (K-F) / SQRT(DTE)
- Moneyness2
- LOG(K/F)
- Normal Model: (K-F)
- Standard Deviation
See FAQ question below with evaluation instructions for details on how to use each equation type.
The following 5-, 10-, 20-, 30- and 60-day realized futures volatility data are available:
- Listed expiration
- Front, second and third rolling contracts
- Constant maturity contracts (interpolated)
For most products we are deriving volatility data for all available, active expirations (this includes active short-dated options in the Ag complex).
For energy products, we will only grab three years of expiration contracts. This is generally the portion of the term structure that has most, if not all, of the open interest. The exception to this three-year window is the Eurodollar product. Most of the ED$ curve have a solid open interest base, so we cover the entire curve.
CME DataMine does not show any of the data graphically, but you can see charts of all the data we offer, as well as other information, via the QuikVol user interface. The QuikVol tool is accessible as part of the QuikStrike Essentials toolbox.
CME DataMine only supports expiration level curve equations at this point.Bantix believes that the strike level data is easy to create with the equation data.
See a sample calculation in the How do I use the curve coefficient data to calculate the strike level volatility? question below.
If you would prefer to download strike level information, email our Data Sales team at cmedatasales@cmegroup.com.
Data can be purchased for a single (or multiple) asset class(es) or for the entire set of asset classes. Data will be delivered/available on a product level basis.
The prices used to create the option volatility curves is a combination of CME Group settlement and SPAN file data. When strike open interest (OI) is available for an expiration (CME DataMine EOD files only contain settlement prices for strikes with OI), this data is used to create the volatility curves. For expirations with little or no OI, the expirations with actual, derived curves will be used to (linearly) interpolate curves for these “empty” expirations.
For data from 2007 through 2010, SPAN file data was used to create volatility curves. Data from 2011 forward, will use EOD settlement data (augmented with SPAN when and if possible).
Strike-based curves are created by using the at-the-money (ATM) straddle implied volatility and all out-of-the-money (OTM) implied volatilities to create a least squares (fourth order) polynomial fit for this set of points. The curve is fit between all available strikes from the -2 to +2 delta range.
Note: For Eurodollars, the curve is always forced to go through the ATM strike. We believe that this is especially important for active contracts with a limited strike range like the Eurodollar contract.
For the other curve types (Delta, Moneyness1, Moneyness2 and Standard Deviation), the strike curve is used to create a set of points that represent the curves’ data. Those points are then fit (in the same fashion mentioned above). Each curve has a low strike and high strike associated with the curve. For the non-strike curves, this strike is a low and high data point on the curve (i.e. Delta, Moneyness, etc.).
Volatility points on the curve can then be calculated by stepping through the points from low to high, or ANY point in between, and evaluating the polynomial equation. One of the strengths of the fitted curve volatility equation is that the user can calculate a volatility for any point on the curve without being limited to a listed strike, fixed delta step, etc.
For expirations with little or no OI, the expirations with actual, derived curves will be used to (linearly) interpolate curves for these empty expirations.
Options continue to trade when a future is locked limit up or down. On days when the futures settle in this state, QuikVol finds the at-the-money strike by looking for the strike where put and call settlement are closest to each other and derives a put-call parity futures price. This price is then used as the futures price input for deriving the implied volatility for the rest of the settlement prices.
No, since data is stored and delivered at the expiration level, strike level data is not available. However, you can get option settlement prices from DataMine as well as a limited date range from Bantix and the QuikStrike tools.
Since our data is delivered at the expiration level, and futures are expiration level products, we do provide the price, volume and open interest as part of each record (for data from 2011 forward only).
The data will be delivered in CSV file format.
There is one record per option expiration tracked and one record for each futures contract (on a per product basis). Therefore, the individual product files are not very large (files sizes range from 2kb to 48kb).
There will be 42 options and 42 futures files that are dispersed over six different asset classes.
Once per day since the information is end-of-day data.
The files will be delivered around 11am Central Time (CT) the following business day.
The files will be compressed.
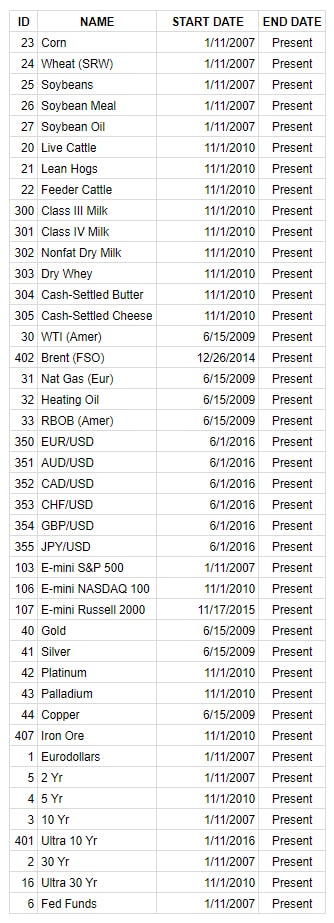
Data is available from January 1, 2007 (or from where the data for a given product starts to be available) and forward. Below is a list of each product and its availability.
We are working on having Bitcoin (BRR or BTC) realized volatility available soon in CME DataMine. In the meantime, QuikVol has this information available.
If you would like access to this information, contact cmedatasales@cmegroup.com QuikStrike also has Bitcoin option volatility curves available.
This is data derived from QuikStrike proprietary calculations.
We use the following formulas for each type of option product:
- American Options
- Bjerksund Stensland 2002
- European Options
- Black 76
- Short-term Interest Rate (STIR) Options
- Bachelier (Normal Price Distribution)
- Average Price Options (APO)
- Curran APO
- Calendar Spread Options
- Bachelier (Normal Price Distribution)
- Agriculture Futures and Options
- Corn
- Chicago Wheat
- Soybeans
- Soybean Oil
- Soybean Meal
- Live Cattle
- Feeder Cattle
- Lean Hogs
- Class III Milk
- Cash-Settled Cheese
- Class IV Milk
- Dry Whey
- Non-Fat Dry Milk
- Cash-Settled Butter
- Energy Futures and Options
- WTI Crude Oil
- Henry Hub Natural Gas
- Brent Last Day Financial
- RBOB Gasoline
- USLD Heating Oil
- Equities Futures and Options
- E-mini S&P 500
- E-mini Nasdaq
- E-mini Russell 2000
- FX Futures and Options
- AUD/USD
- CAD/USD
- EUR/USD
- GBP/USD
- JPY/USD
- CHF/USD
- Metals Futures and Options
- Gold
- Silver
- Copper
- Platinum
- Palladium
- Iron Ore
- Interest Rates Futures and Options
- Eurodollars
- US 2-Year Note
- US 5-Year Note
- US 10-Year Note
- US Ultra 10-Year Note
- US 30-Year Long Bond
- US Ultra Treasury Bond
- Fed Funds

Here is one example of how Bantix reaches the delta-based curve (but all curves are evaluated in the same fashion). For purposes of our example, we used the delta because we believe that it is the most generic across all products. The PutDeltaLow column, with a value of 0.05, represents the 5-delta put. To continue the volatility curve evaluation, step up (with 0.05 delta increments) to the 0.10 (10-Delta put), 0.15 (15-Delta put) etc. until you get to the PutDeltaHigh or 0.95 value (5-Delta call). The at-the-money (ATM) volatility is the 0.50 value (makes sense right). You can use any delta value to evaluate a volatility at a given point but the spreadsheet example is a typical calculation method for creating a delta-based curve.
And, our other curves follow in the same fashion. You will start with the low strike, money-ness or standard deviation value and step up by a strike increment, or other decimal value for the money-ness and standard deviation values until you get to or near the high value. However, to reiterate, you can use any value between the low and high values to evaluate a point on the curve.
Note: Our curves are created to be calculated between the low and high values. If you attempt to evaluate a point outside that range, you may not get a proper value (this is a function of curve fitting in general). However, we have found that this is generally not the case on delta-based curves and does not happen all that often. What we typically do to combat any potential issue we find is the following:
- Use the final left or right value and evaluate the strike outside this range at that volatility value OR
- Find the difference between the last two strikes on both sides and calculate some sort of interpolation (usually linear) and step through the strikes with this increment for further evaluation outside the given range
Download QuikVol Options sample file
| Field Name | Value | Type | Description |
|---|---|---|---|
| Date | 6/12/2018 | Date String | Trade Date |
| Symbol | LOQ18 | String | Listed, Constant Maturity or Rolling Contract Symbol |
| ExpDate | 7/17/2018 | Date String | Contract Expriation Date, if any |
| DTE | 35 | Decimal | Days to Expiration |
| Strike | 66.5 | Decimal | ATM Strike Price |
| Vol | 0.240515356 | Decimal | ATM Volatility |
| Future | 66.28 | Decimal | Future Price used for calculations |
| StrikeLow | 81.5 | Decimal | Lowest strike price to be used to evaluate equation |
| StrikeHigh | 55 | Decimal | Highest strike price to be used to evaluate equation |
| S0 | -4.180410459 | Decimal | Coefficient for x0 term in polynomial equation |
| S1 | 0.303325116 | Decimal | Coefficient for x1 term in polynomial equation |
| S2 | -0.007175166 | Decimal | Coefficient for x2 term in polynomial equation |
| S3 | 0.00007049 | Decimal | Coefficient for x3 term in polynomial equation |
| S4 | -0.00000024 | Decimal | Coefficient for x4 term in polynomial equation |
| DeltaLow | 0.05 | Decimal | Lowest delta value to be used to evaluate equation |
| DeltaHigh | 0.95 | Decimal | Highest delta value to be used to evaluate equation |
| D0 | 0.302841994 | Decimal | Coefficient for x0 term in polynomial equation |
| D1 | -0.490802354 | Decimal | Coefficient for x1 term in polynomial equation |
| D2 | 1.567278943 | Decimal | Coefficient for x2 term in polynomial equation |
| D3 | -2.230388561 | Decimal | Coefficient for x3 term in polynomial equation |
| D4 | 1.139980033 | Decimal | Coefficient for x4 term in polynomial equation |
| MoneynessLow | 0.034941183 | Decimal | Lowest moneyness value to be used to evaluate equation |
| MoneynessHigh | -0.031533552 | Decimal | Highest moneyness value to be used to evaluate equation |
| M0 | 0.240515356 | Decimal | Coefficient for x0 term in polynomial equation |
| M1 | -0.676923052 | Decimal | Coefficient for x1 term in polynomial equation |
| M2 | 58.69151794 | Decimal | Coefficient for x2 term in polynomial equation |
| M3 | 665.7074633 | Decimal | Coefficient for x3 term in polynomial equation |
| M4 | 3570.269464 | Decimal | Coefficient for x4 term in polynomial equation |
| Moneyness2Low | 1.229631865 | Decimal | Lowest moneyness value to be used to evaluate equation |
| Moneyness2High | 0.829812915 | Decimal | Highest moneyness value to be used to evaluate equation |
| M2-0 | 0.240515356 | Decimal | Coefficient for x0 term in polynomial equation |
| M2-1 | 2.680643891 | Decimal | Coefficient for x1 term in polynomial equation |
| M2-2 | -5.916905488 | Decimal | Coefficient for x2 term in polynomial equation |
| M2-3 | 3.898370877 | Decimal | Coefficient for x3 term in polynomial equation |
| M2-4 | -0.66315935 | Decimal | Coefficient for x4 term in polynomial equation |
| STDLow | 81.5 | Decimal | Lowest standard deviation value to be used to evaluate equation |
| STDHigh | 55 | Decimal | Highest standard deviation value to be used to evaluate equation |
| STD0 | -27.81891693 | Decimal | Coefficient for x0 term in polynomial equation |
| STD1 | 0.799309677 | Decimal | Coefficient for x1 term in polynomial equation |
| STD2 | -0.008882334 | Decimal | Coefficient for x2 term in polynomial equation |
| STD3 | 0.00005823 | Decimal | Coefficient for x3 term in polynomial equation |
| STD4 | -0.00000016 | Decimal | Coefficient for x4 term in polynomial equation |
Download QuikVol Futures sample file
| Field Name | Value | Type | Description |
|---|---|---|---|
| Date | 6/21/2018 | Date String | Trade Date |
| Symbol | TYU18 | String | Listed, Constant Maturity or Rolling Contract Symbol |
| ExpDate | 9/19/2018 | Date String | Contract Expriation Date, if any |
| DTE | 90 | Decimal | Days to Expiration |
| Open | 119.5 | Decimal | Opening Price |
| High | 119.921875 | Decimal | High Price |
| Low | 119.421875 | Decimal | Low Price |
| Settle | 119.859375 | Decimal | Settlement Price |
| Volume | 1566709 | Decimal | Contract Volume |
| OI | 3469995 | Decimal | Contract Open Interest |
| HV5 | 0.030838871 | Decimal | 5-Day Historical Realized Volatility |
| HV10 | 0.027059581 | Decimal | 10-Day Historical Realized Volatility |
| HV20 | 0.059439273 | Decimal | 20-Day Historical Realized Volatility |
| HV30 | 0.053671814 | Decimal | 30-Day Historical Realized Volatility |
| HV60 | 0.043493566 | Decimal | 60-Day Historical Realized Volatility |
Neither futures trading nor swaps trading are suitable for all investors, and each involves the risk of loss. Swaps trading should only be undertaken by investors who are Eligible Contract Participants (ECPs) within the meaning of Section 1a(18) of the Commodity Exchange Act. Futures and swaps each are leveraged investments and, because only a percentage of a contract’s value is required to trade, it is possible to lose more than the amount of money deposited for either a futures or swaps position. Therefore, traders should only use funds that they can afford to lose without affecting their lifestyles and only a portion of those funds should be devoted to any one trade because traders cannot expect to profit on every trade.
CME Group, the Globe Logo, CME, Globex, E-Mini, CME Direct, CME DataMine and Chicago Mercantile Exchange are trademarks of Chicago Mercantile Exchange Inc. CBOT is a trademark of the Board of Trade of the City of Chicago, Inc. NYMEX is a trademark of New York Mercantile Exchange, Inc. COMEX is a trademark of Commodity Exchange, Inc. All other trademarks are the property of their respective owners.